Issue 2 (190)/2022

ALSE and ACS Style
Sfîru, R.; Cardei, P.; Muraru-Ionel, C.; Muraru, V. Supplements to the problem of energy consumption in reducing lignocelluloses biomass size to produce energy. Journal of Applied Life Sciences and Environment 2022, 55 (2), 159-165.
https://doi.org/10.46909/alse-552054

AMA Style
Sfîru R, Cardei P, Muraru-Ionel C, Muraru V. Supplements to the problem of energy consumption in reducing lignocelluloses biomass size to produce energy. Journal of Applied Life Sciences and Environment. 2022; 55 (2): 159-165.
https://doi.org/10.46909/alse-552054

Chicago/Turabian Style
Sfîru, Raluca, Petru Cardei, Cornelia Muraru-Ionel, and Vergil Muraru. 2022. “Supplements to the problem of energy consumption in reducing lignocelluloses biomass size to produce energy” Journal of Applied Life Sciences and Environment 55, no. 2: 159-165.
https://doi.org/10.46909/alse-552054

Supplements to the Problem Of Energy Consumption in Reducing Lignocelluloses Biomass Size to Produce Energy

Raluca SFÎRU, Petru CARDEI, Cornelia MURARU-IONEL and Vergil MURARU*

National Institute of Research, Development for Machines and Installations designed to Agriculture and Food Industry, INMA Bucharest, 6, Ion Ionescu de la Brad Blv. Sector 1, Bucharest, 013813, Romania; e-mail: raluca_sfiru@yahoo.com, petru_cardei@yahoo.com, cornelia.muraru.ionel@yahoo.com

*Correspondence: virgil.muraru@gmail.com 

Received: Nov. 22, 2022. Revised: Dec. 25, 2022. Accepted: Jan. 04, 2022. Published online: Jan. 26, 2023

ABSTRACT. This article presents complementary results on experimental data on the process of reducing the size of plant biomass by mechanical cutting. According to the source of the experimental data, the problem of statistical modelling of the main parameters describing the process of biomass reduction was approached. A more comprehensive formulation of the list of main system parameters was also attempted, which should be considered in a minimal mathematical model. The results of this article are starting points for a systemic approach to this biomass processing process. A first systematization is fixing 13 parameters that are included in the model of the biomass size reduction phenomenon. The 13 model parameters are divided into three categories: input parameters (5), adjustment parameters (4) and output parameters (4).

The performances of the interpolation formulas are evaluated using the global error and the maximum error, varying between 1% and 0.1% for the prior and 3.8% and 0.34% for the latter. Some mathematical models suggest the existence of optimal operating points. Their exploitation can only come as a result of new high-resolution experimental research, at least in terms of rotation speed.

Keywords: qualitative; characteristics; biomass; size; reduction.

INTRODUCTION

This article is written as an extension (mathematical supplement to the technological process) of the results presented in Moiceanu et al. (2019) using experimental data obtained and published by the authors of the same article. Obtaining a theoretical, experimental or theoretical-experimental mathematical model involves the use of experimental data not only for modelling but also for validation. We took advantage of the experimental data published in Moiceanu et al. (2019) to initiate a new stage of statistical modelling of the process of reducing biomass size by mechanical means, but also to formulate a more comprehensive picture of the parameters characterizing the system involved in the process.

To describe the current results in the field of reducing biomass size by mechanical means, we can see the introduction from Moiceanu et al. (2019), which is not necessary to reiterate. Regarding the cost-effectiveness of the plant biomass processing operations discussed in Moiceanu et al. (2019), a very high economic study considers various factors, from the energy content, the calorific value of the biomass to the costs of transportation, storage and use of lighters manufactured from the biomass. All the features must ultimately be converted into money. The economic aspect and the overall energy efficiency is not addressed in this article. The subject of the article is extensively addressed in works such as Akhtar et al. (2019). Characteristics of lignocellulose, chemical and physical properties, as well as aspects of industrial processing are presented in Anwar et al. (2014). Results of the research on the use of lignocellulosic wastes used below their value as sources of raw material for biofuel are presented in Adewuyi (2022). Methods for pretreatment of lignucellulosic biomass are presented in Kumar et al. (2009). The influence of lignocellulosic biomass variability on the size reduction process is exposed in Oyedeji et al. (2020) using research from many papers on this issue. Regarding energy consumption to reduce the size of lignocellulose, some results are also given in Miao et al. (2014) and Zhu et al. (2010).

MATERIALS AND METHODS

The results presented in this article were obtained using the experimental material provided in Moiceanu et al. (2019). A comparative analysis of the experimental results was obtained by grinding multiple types of plant biomass (miscanthus, corn stalks, alfalfa, willow) used in the process of bio-refining and bio-fracturing (Moiceanu et al., 2019).

Looking at the biomass mill as a system, its parameters can be classified into:

• input parameters:
  • mass material;
  • type of material;
  • material quantity;
  • density of the material;
  • thermo-mechanical characteristics of the material (which also depend on humidity);
• operation setting parameters:
  • the speed of rotation of the cutting elements (note ω);
  • load of material loading;
  • the average size of the material entered into the process;
  • the working temperature;
• and output parameters:
  • distribution of processed material, by size;
  • a measure of the degree of reduction (note d_m);
  • working capacity;
  • energy consumption per unit mass of material (note ε)

The model proposed by Moiceanu et al. (2019) uses only three of the listed parameters: the speed of rotation of the cutting elements (note ω), energy consumption per unit mass of material (note ε) and a measure of the degree of reduction, named grinding degree (note d_m). The method of direct or indirect measurement of the three parameters is described in Moiceanu et al. (2019).

RESULTS AND DISCUSSION

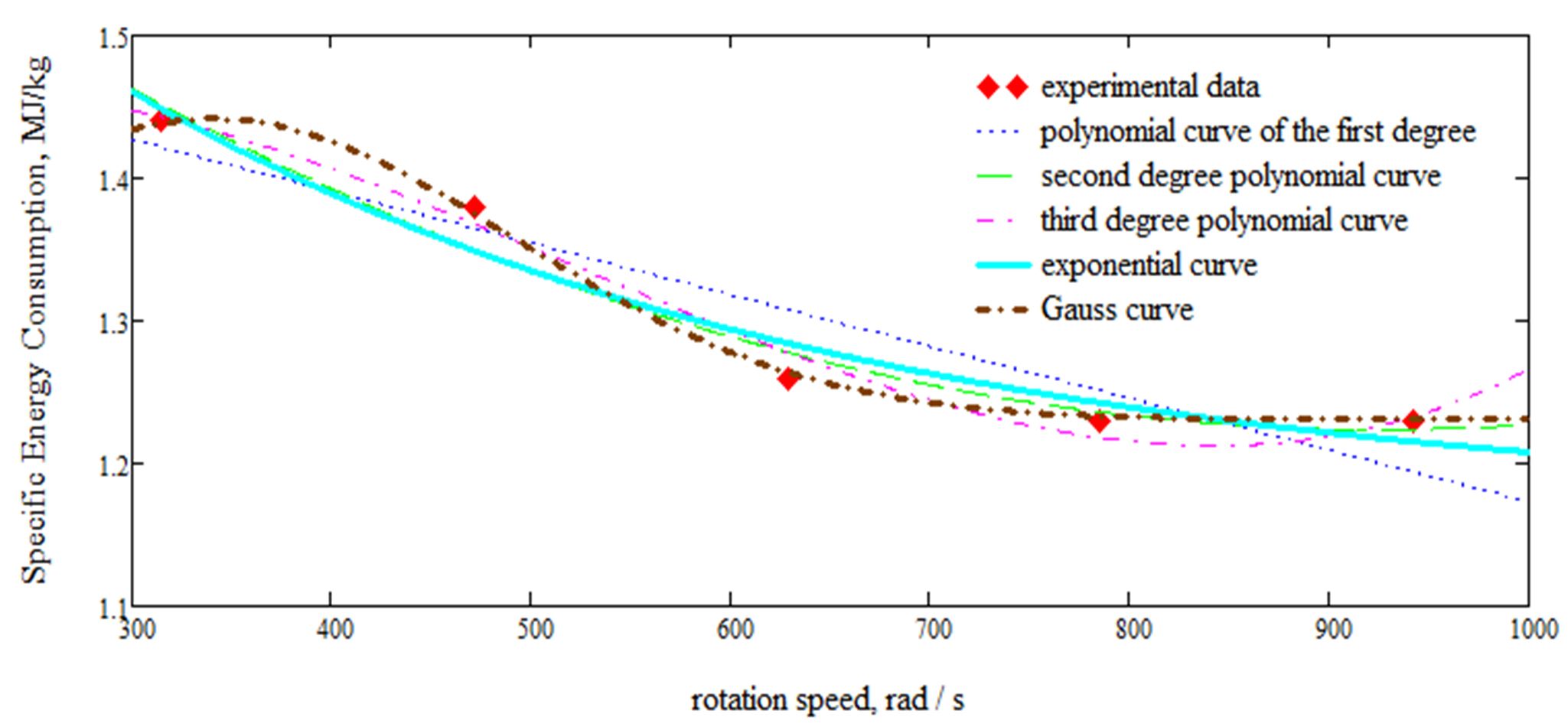
The data published in Tables 1 and 2 of Moiceanu et al. (2019) allow interpolation of the energy consumption per unit mass of material and the degree of reduction as functions of the rotation speed of the cutter. Using interpolation techniques from Degeratu (2001), the following interpolated functions for the energy consumption per unit mass of material were obtained to reduce alfalfa size (Eqs. 1-5):

ε(ω) = 1.536 – 0.0003629ω                    (1)

for the first-degree interpolation polynomial,

ε(ω)=1.746 – 0.001127ω+0.0000006079ω² (2)

for the second-degree interpolation polynomial, 

for the third-degree interpolation polynomial,

ε(ω) = 0.676e^-0.002762ω +1.165                 (4)

for the simple exponential curve,

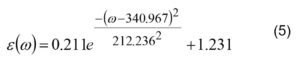for the Gauss curve.

The graphical representation of the five curves obtained by interpolation is given in Figure 1, along with the experimental data. Some measures of the approximation error of interpolation functions are given in Table 1. The measures of interpolation function errors relative to experimental data were calculated according to Eq. 6 and Eq. 7.

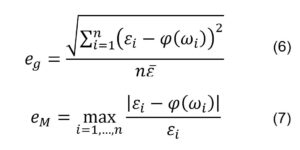
where e_g is the global error measure and e_M is the maximum error measure for the energy consumption per unit mass of material, ε_i are the experimental data of the energy consumption per unit mass of material, n is the number of data, ω_i are the rotation speeds of the knife’s experimental values and φ is the interpolation function for the energy consumption per unit mass of material. Similar formulas we used for the degree of reduction.

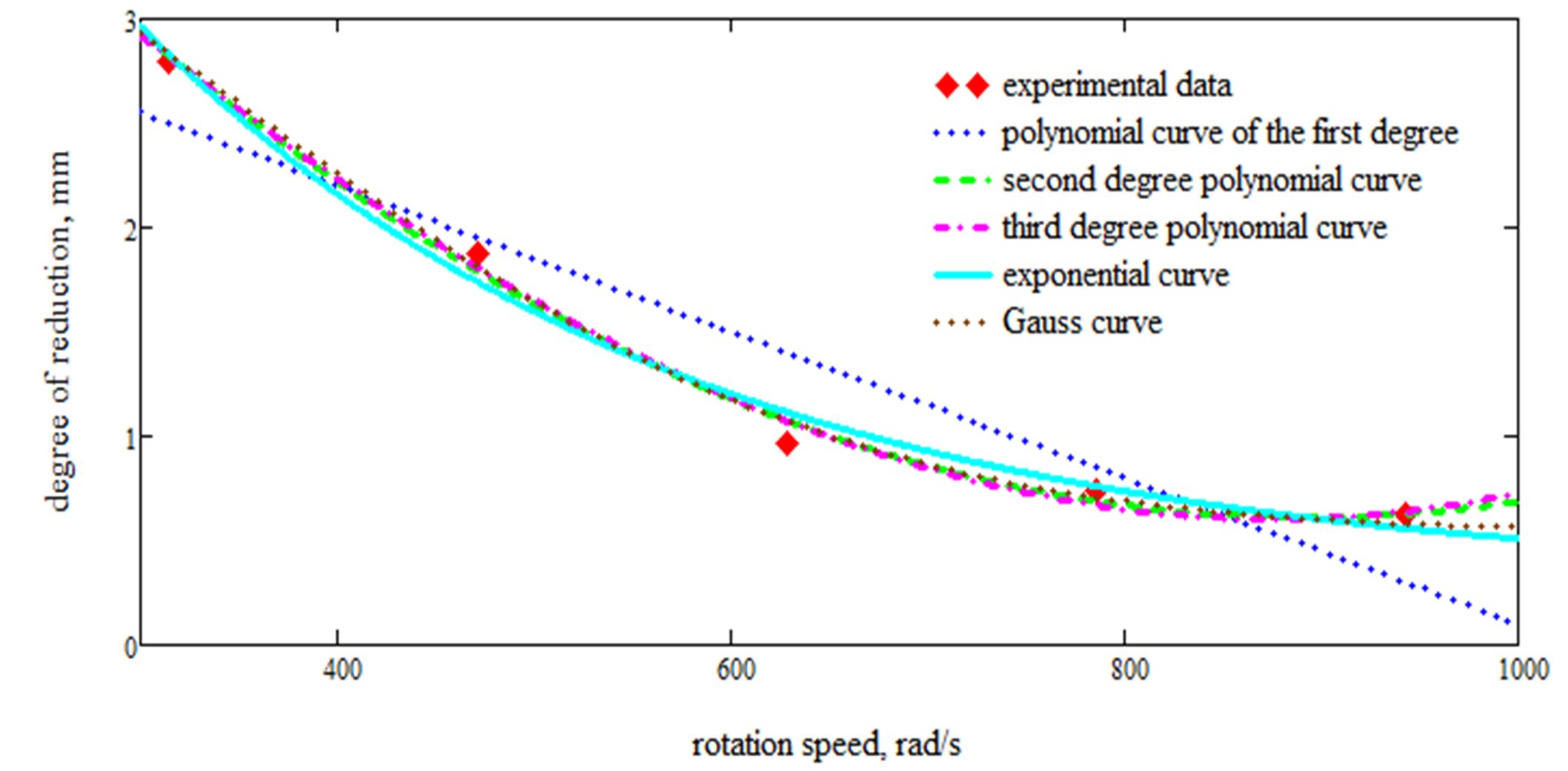
Similarly, the interpolation curves of the degree of reduction of the rotation speeds of the knives are obtained by Eqs. 8-12:

d_m(ω) = 3.602 – 0.0003501ω                 (8)

 for the first-degree interpolation polynomial, 

for the second-degree interpolation polynomial, 

for the third-degree interpolation polynomial,

d_m(ω) = 7.858e^-3591ω+0.293                (11)

for the simple exponential curve, and

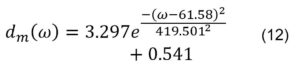
for the Gauss curve. The interpolated curves (8)–(12) are graphically represented in Figure 2.

Figure 1 – Specific energy consumption dependent on cutter rotation speed, according to the five interpolation curves used

Figure 2 – The degree of reduction dependence on cutter rotation speed, according to the five interpolation curves used

Table 1
The interpolation errors for each of the five interpolation curves of the dependence between specific energy consumption and the rotation speeds of the cutters

Table 2
The interpolation errors for each of the five interpolation curves of the dependence between reducing degree and rotation speed of the cutters.

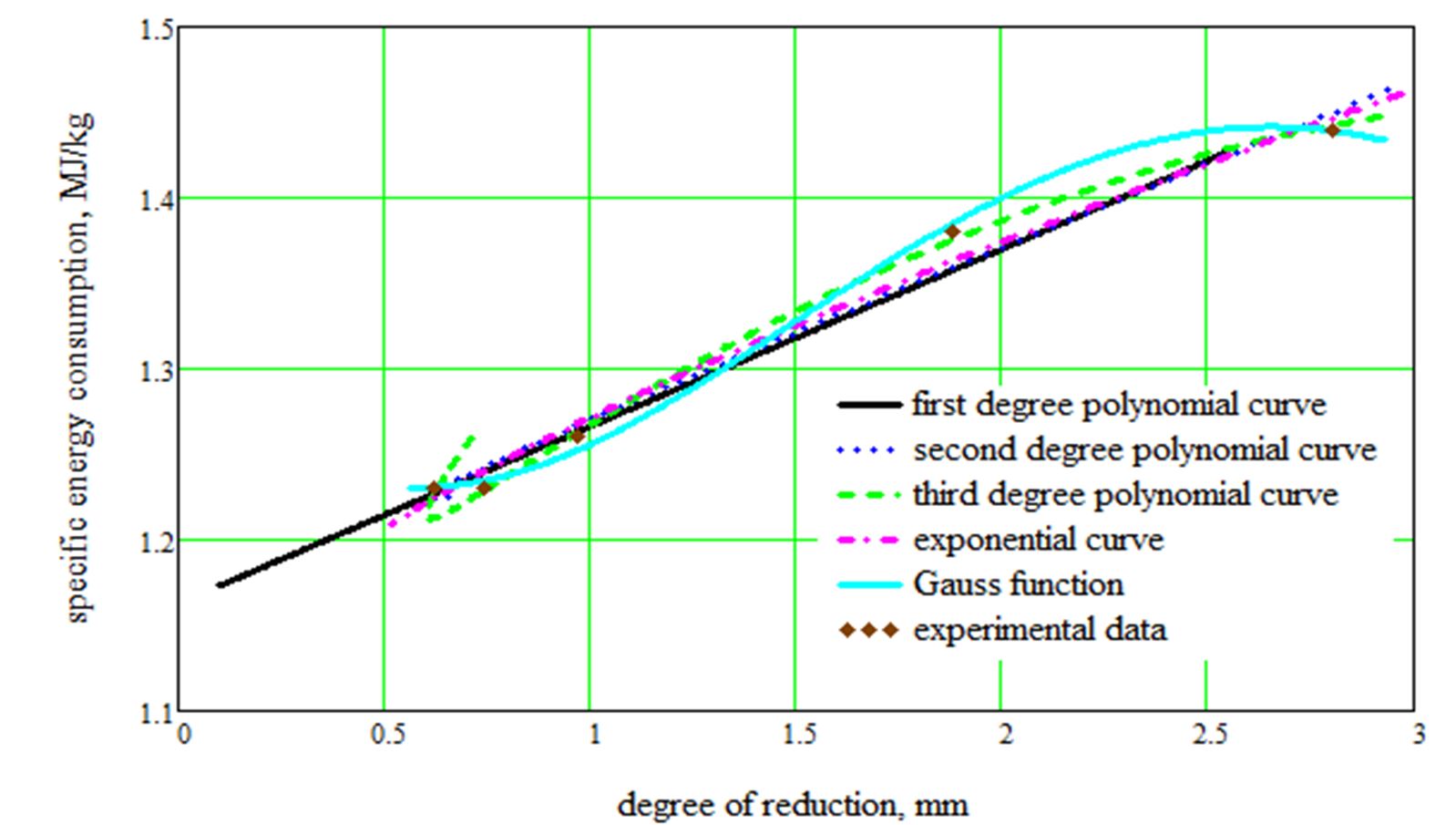
If the specific energy and the degree of reduction are considered qualitative characteristics of the chopping process, in Figure 3 a graphical picture of the qualitative behaviour of the system is given. Generally, regardless of the type of interpolation curve, it is noted that obtaining a small specific consumption implies a low degree of reduction (qualitatively favourable). The fulfilment of these conditions in the working process, according to the variations of the specific energy consumption and the degree of reduction (Figure 1 and Figure 2), takes place for the high rotational speeds of the cutter.

Figure 3 – A graphic representation in the quality plan of the process of reducing the size of plant material: specific energy consumption – degree of reduction

Generally, regardless of the type of interpolation curve, obtaining a small specific consumption implies a low degree of reduction (qualitatively favourable). The fulfilment of these conditions in the working process, according to the variations of the specific energy consumption and the degree of reduction (Figure 1 and Figure 2), takes place for the high rotational speeds of the cutter. Similar results can be obtained for the other two types of biomasses for which experimental results are given in Moiceanu et al. (2018): miscanthus and corn stalks.

The relationship given by the dimensional analysis of the three parameters that are varied in the experiments described in Moiceanu et al. (2018) is in accordance with Degeratu, 2015, for example, given by the following Eq. 13:

where 𝑘 is a modelling constant. For the degree of reduction, a form of dependence on rotational speed (Eqs. 8 – 12) was deduced from the experimental results. Thus, relationship (13) becomes (14)

This latest model is not more accurate than the previous ones.

CONCLUSIONS

Statistical mathematical modelling by interpolation and other types of statistical analysis is a necessary step for a functional description of any processing or system process. A functional picture, once established and validated, allows for improved operating conditions or even optimization of the working regime.

For the experimental results we operated on, the statistical modelling presented in this article confirms the experimental functional dependencies. Specific energy consumption decreases with increasing spin speed of knives. The reduction degree decreases when the speed of rotation of the knives increases (biomass is better crushed).

The choice of interpolation functions will be made considering their precision and/or the physical significance of the parameters involved.

A refinement stage of the modelling results will focus on the use of dimensionless combinations of parameters in interpolation functions. This approach is facilitated by a preliminary dimensional analysis of the parameters defining the system. To obtain a satisfactory prediction accuracy, it is necessary to consider a larger number of parameters involved in the process.

Author Contributions:  conceptualization: R.S., P.C., C.M., V.M.; methodology: R.S., P.C., C.M., V.M.; analysis: R.S., P.C., C.M., V.M.; investigation: R.S., P.C., C.M., V.M.

resources: R.S., P.C., C.M., V.M.; data curation: R.S., P.C., C.M., V.M.; writing: R.S., P.C., C.M., V.M.; review: R.S., P.C., C.M., V.M.; supervision and so on: P.C, V.M.

All authors declare that they have read and approved the publication of the manuscript in this present form.

Acknowledgement: The authors would wish to express their gratitude to “Ministerul Cercetării şi Inovării” trough project 1 PFE/30.12.2021 and project PN 19 10 01 02.

Conflicts of Interest: There are no conflicts of interest.

REFERENCES

Adewuyi, A. Underutilized Lignocellulosic Waste as Sources of Feedstock for Biofuel Production in Developing Countries. Frontiers in Energy Research. 2022, 10, 741570. https://doi.org/10.3389/fenrg.2022.741570.

Akhtar, N.; Gupta, K.; Goyal, D.; Goyal, A. Lignocellulosic biomass charateristics for bioenergy application: an overview. Environmental Engineering and Management Journal. 2019, 18, 367-383.

Anwar, Z.; Gulfraz, M.; Irshad, M. Agro-industrial lignocellulosic biomass a key to unlock the future bio-energy: A brief review. Journal of Radiation Research and Applied Sciences. 2014, 7, 163-173. https://doi.org/10.1016/j.jrras.2014.02.003.

Degeratu, M. Dimensional analysis, similarity and modelling (in Romanian), Romanian Academy of Science Publishing House Bucharest, Romania, 2015.

Kumar, P.; Barrett, D.M.; Delwiche, M.J.; Stroeve, P. Methods for Pretreatment of Lignucellulosic Biomass for Efficient Hydrolysis and Biofuel Production. Industrial & Engineering Chemistry Research. 2009, 48, 3713-3729. https://doi.org/10.1021/ie801542g.

MathSoftMath Soft Engineering & Education, Mathcad User’s Guide with Reference Manual Mathcad 2001 Professional, Cambridge: MathSoftMath Soft Engineering & Education, Inc., 2001.

Miao, Z.; Grift, T.E.; Ting, K.C. Size Reduction and Densification of Lignocellulosic Biomass Feedstock for Biopower, Bioproducts, and Liquid Biofuel Production. Encyclopedia of Agricultural, Food, and Biological Engineering, Second Edition. https://doi.org/10.1081/E-EAFE2-120051298.

Moiceanu, G.; Paraschiv, G.; Voicu, G.; Dinca, M.; Negoita, O.; Chitoiu, M.; Tudor, P. Energy Consumption at Size Reduction of Lignocellulose Biomass for Bioenergy. Sustainability. 2019, 11, 2477. https://doi.org/10.3390/su11092477.

Oyedeji, O.; Gitman, P.; Qu, J.; Webb, E. Understanding the Impact of Lignocellulosic Biomass Variability on the Size Reduction Process: A Review. ACS Sustainable Chemistry & Engineering. 2020, 8, 2327-2343. https://doi.org/10.1021/acssuschemeng.9b06698.

Zhu, W.; Zhu, J.Y.; Gleisner, R.; Pan, X.J. On energy consumption for size-reduction and yields from subsequent enzymatic saccharification of pretreated lodgepole pine. Bioresource Technology. 2010, 101, 2782-2792. http://dx.doi.org/10.1016/j.biortech.2009.10.076.

Academic Editor: Dr. Isabela Maria Simion

Publisher Note: Regarding jurisdictional assertions in published maps and institutional affiliations ALSE maintain neutrality.